演習問題　その４

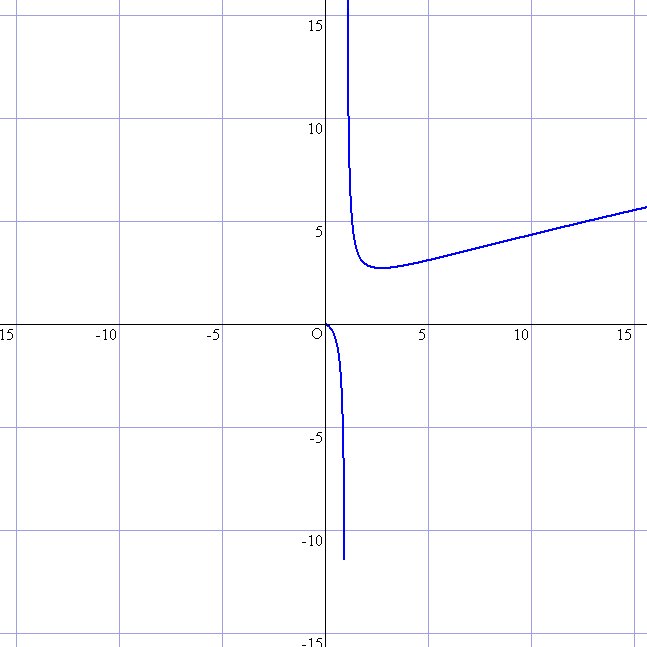
y=x/logxのグラフを書け。

１、定義域
　　対数の真数の定義により、logxのxは正である必要があるから、x>0
    また、分母≠0より、logx≠0。よって、x≠1。

　　　　答え　x>0 かつ　x≠1

２、増減表
　　y=f(x)とおくと
       f'(x)=-1/(logx)2+1/logx
    f'(x)より
　　　 -1/(logx)2+1/logx=0
       (logx)2=logx
       logx(logx-1)=0
    logx≠0であるから、logx=1
    よって、x=e
    したがって、増減表は以下のようになる
　　

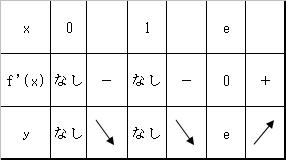３、極値、凹凸、極限(４箇所)
    極値  上の増減表より、x=eのとき、y=e

    凹凸　f''(x)=-2/x(logx)3+1/x(logx)2
                =(-2+logx)/x(logx)3
          f''(x)=0とおくと
　　　　　　　　logx=2
                   x=e2　(ちょっとあやしい)
          よって、・・・・

    極限　limx→0f(x)=0/-∞=-0    
          limx→-1f(x)=-∞ (なぜなら、0＜x＜1のとき、logx＜0)
          limx→+1f(x)=+∞ (なぜなら、x＞1のとき、logx＞0)
          limx→+∞f(x)=+∞

４、極値、変曲点

したがって、グラフは次のようになります。